Drew Wilimitis

It has been recently established that many real-world networks have a latent geometric structure that resembles negatively curved hyperbolic spaces. Therefore, complex networks, and particularly the hierarchical relationships often found within, can often be more accurately represented by embedding graphs in hyperbolic geometry, rather than flat Euclidean space.

The goal of this project is to provide Python implementations for a few recently published algorithms that leverage hyperbolic geometry for machine learning and network analysis. Several examples are given with real-world datasets, however; the time complexity is far from optimized and this repository is primarily for research purposes - specifically investigating how to integrate downstream supervised learning methods with hyperbolic embeddings.

Contents

Models

• Poincaré Embeddings:
  • Mostly an exploration of the hyperbolic embedding approach used in [1].
  • Available implementation in the gensim library and a PyTorch version released by the authors here.
• Hyperbolic Multidimensional Scaling: nbviewer
  • Finds embedding in Poincaré disk with hyperbolic distances that preserve input dissimilarities [2].
• K-Means Clustering in the Hyperboloid Model: nbviewer
  • Optimization approach using Frechet means to define a centroid/center of mass in hyperbolic space [3, 4].

  

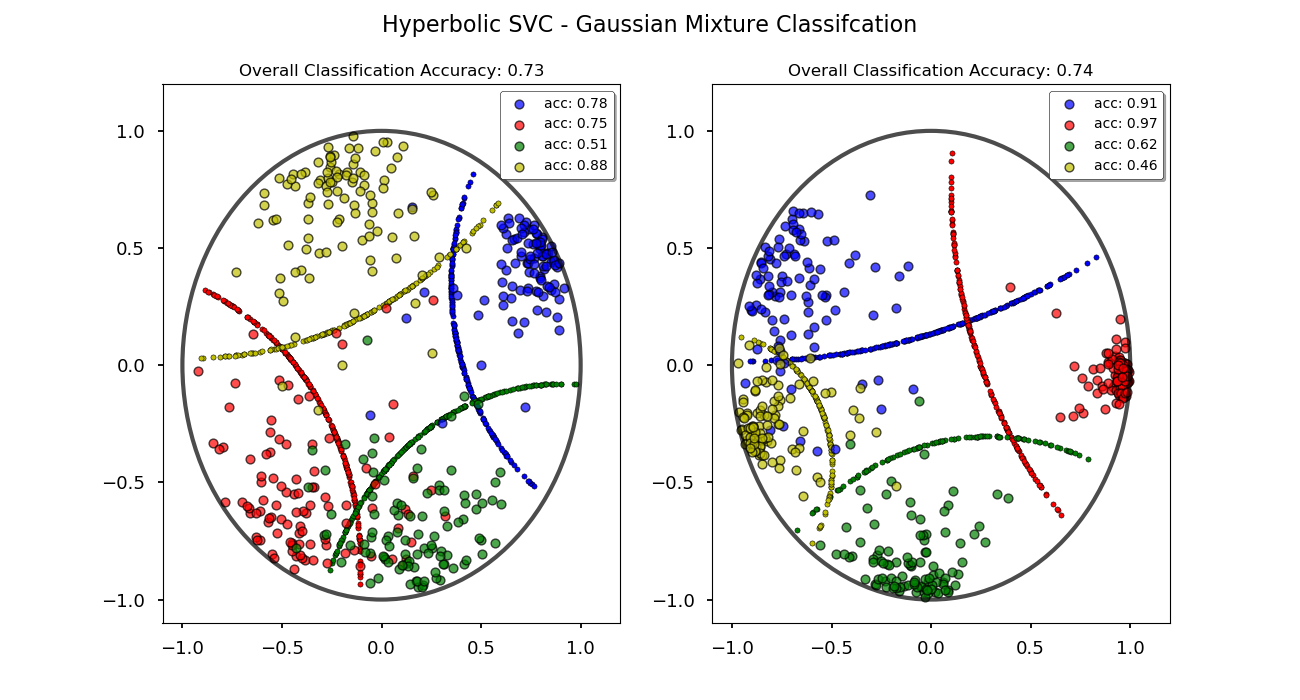
• Hyperbolic Support Vector Machine - nbviewer
  • Linear hyperbolic SVC based on the max-margin optimization problem in hyperbolic geometry [5].
  • Uses projected gradient descent to define decision boundary and predict classifications.

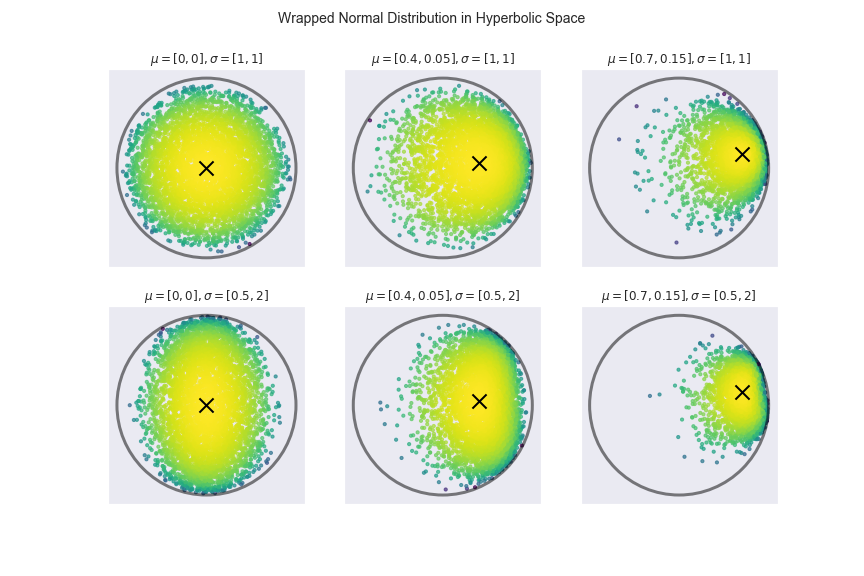
• Hyperbolic Gaussian Mixture Models - nbviewer

  • Iterative Expectation-Maximization (EM) algorithm used for clustering [6].
  • Wrapped normal distribution based on using parallel transport to map to hyperboloid

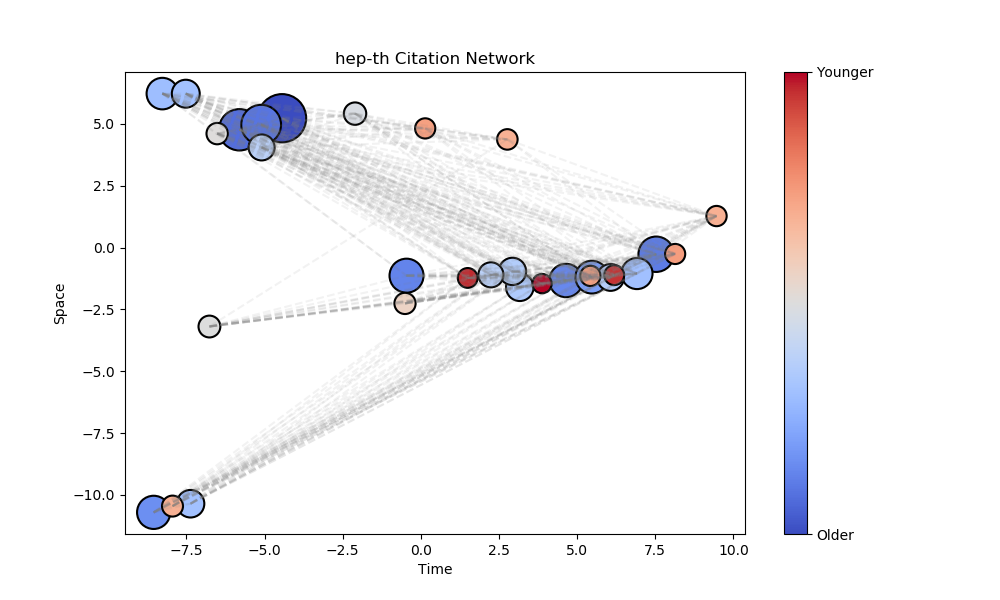
• Embedding Graphs in Lorentzian Spacetime - nbviewer

  • An algorithm based on notions of causality in the Minkowski spacetime formulation of special relativity [7].
  • Used to embed directed acyclic graphs where nodes are represented by space-like and time-like coordinates.

• Application: fMRI Schizophrenia Classification - nbviewer

  • Deriving hyperbolic features from functional network connectomes and predicting schizophrenia.
  • Analyzing discriminating factors from coalescent embeddings and hyperbolic kmeans clustering

Datasets

• Zachary Karate Club Network
• WordNet
• Enron Email Corpus
• Polbooks Network
• arXiv Citation Network
• Synthetic generated data (sklearn.make_datasets, networkx.generators, etc.)

Dependencies

• Models are designed based on the sklearn estimator API (sklearn generally used only in rare, non-essential cases)
• Networkx is used to generate & display graphs

References

[1] Nickel, Kiela. “Poincaré embeddings for learning hierarchical representations” (2017). arXiv.

[2] A. Cvetkovski and M. Crovella. Multidimensional scaling in the Poincaré disk. arXiv:1105.5332, 2011.

[3] “Learning graph-structured data using Poincaré embeddings and Riemannian K-means algorithms”. Hatem Hajri, Hadi Zaatiti, Georges Hebrail (2019) arXiv.

[4] Wilson, Benjamin R. and Matthias Leimeister. “Gradient descent in hyperbolic space.” (2018).

[5] “Large-margin classification in hyperbolic space”. Cho, H., Demeo, B., Peng, J., Berger, B. CoRR abs/1806.00437 (2018).

[6] Nagano, Yoshihiro et al. “A Differentiable Gaussian-like Distribution on Hyperbolic Space for Gradient-Based Learning.” ArXiv abs/1902.02992 (2019)

[7] Clough JR, Evans TS (2017) Embedding graphs in Lorentzian spacetime. PLoS ONE 12(11):e0187301. https://doi.org/10.1371/journal.pone.0187301.